By Dr. Tobias Hahn, Principal Scientist at Cytiva
Introduction
In recent decades, computer simulation has become an indispensable tool in many industries. In the automotive and aerospace industries, for example, simulation has enabled significantly shorter innovation cycles and an increase in productivity. The chemical industry has also benefited from this development. Despite the innovative nature of the biopharmaceutical industry, bioprocess development is only starting to establish simulation-based workflows.
Many in the bioprocess industry agree that expensive and time-consuming laboratory experiments, iterative empirical optimization, and even statistical methods alone are not the answer to the challenges of the future. Many global biopharma companies are working on establishing digital twins of their upstream or downstream processes. Regulatory authorities are encouraging these developments: when the European Medicines Agency (EMA) and the US Food and Drug Administration (FDA) started requesting a deeper understanding of the production process in the quality-by-design (QbD) initiative, models and computer simulations were explicitly mentioned as the best options to prove mechanistic process understanding (1).
Types of digital twins
Digital twins are virtual representations of real-world systems. When fully implemented, the real and virtual systems are meant to exchange information such that the virtual system mimics precisely the real system’s state. Digital twins can be built using statistical or mechanistic models. Statistical approaches such as big data, machine learning, and artificial intelligence utilize statistics to predict trends and patterns. These methods learn from experience, provided in the form of data. The first QbD approval of a biopharmaceutical (Gazyva™, Genentech) relied heavily on statistical modeling, such as design of experiments (DoE) (2).
The drawback of statistical modeling is that the process design space must be carefully screened using dozens, or even hundreds, of experiments to capture the system dynamics. These dynamics are typically captured in a response-surface model that enables building of a digital twin that can cope with the parameter variations it was trained with. Mechanistic models, in contrast, naturally apply these system dynamics, as they are based on physical and biochemical principles. Less experimental data are needed to calibrate the model for a particular process. Therefore, the mechanistic model can also describe the system dynamics in scenarios it was not calibrated with, possibly beyond the process design space. Consequently, digital twins built from mechanistic models can cope with unexpected deviations.
Inner workings of a mechanistic model
Mechanistic modeling is primarily applied in downstream processing, where a deep understanding of the physical principles already exists. One of the applications with a high demand for better process understanding is chromatography. Chromatography is a complex superimposition of different effects: basic fluid dynamics, mass transfer phenomena, and thermodynamics of phase equilibria.
Figure 1 depicts the basic driving mechanisms in a chromatographic column. Injected components (orange dots in Fig 1) move within the mobile phase. This movement may be caused by different mechanisms; outside the particles’ pores, these injected components are transported by convection and dispersion. Convection is induced by a connected pump. Dispersion comprises wall effects, molecular diffusion, and other mechanisms. A feedstock component can enter the mobile phase within the particle’s pore volume where its movement is dominated mainly by diffusion. Eventually, the component can be adsorbed on to the inner surface of the particle.
When completing a chromatography model, one must also consider the adsorption of components onto the inner surfaces of the adsorber beads. Prevalent models describe the concentration of adsorbed species as a function of the species concentrations in the mobile phase of the particle’s pores (or micro pores of membranes) and the mobile phase composition (ionic strength, pH, etc). Specialized simulation software, such as GoSilico™ Chromatography Modeling Software, offer a variety of models for ion-exchange, hydrophobic interaction, and mixed-mode chromatography.
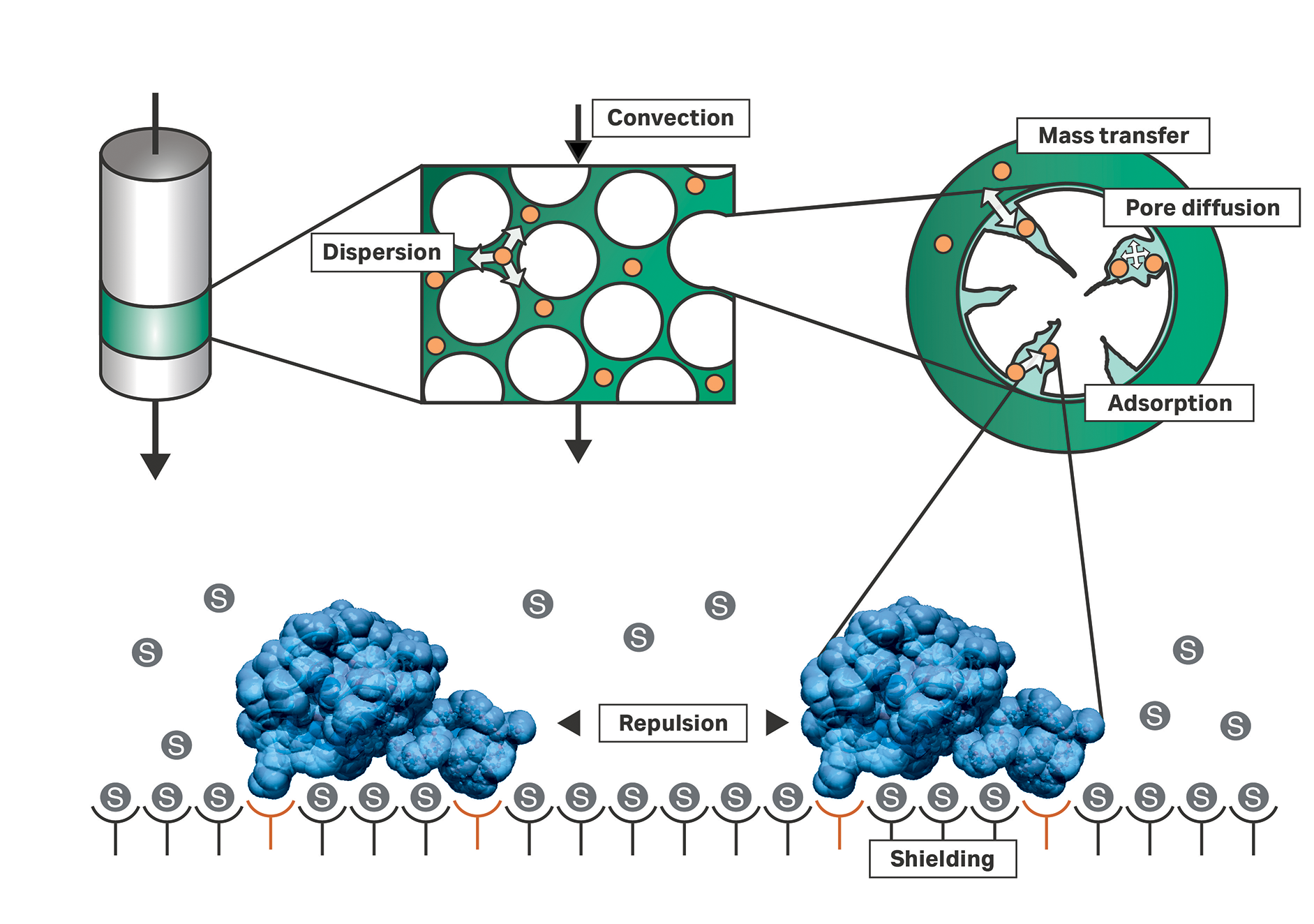
Fig 1. The basic driving mechanisms in a chromatographic column. The chromatogram is a result of fluid dynamic and thermodynamic processes taking place in the volume between adsorber particles (dark green), in the adsorber's pores (light green), and on the adsorber's surface (white). Different models describe the effects in various levels of detail and for different interaction modes, such as ion-exchange or hydrophobic interaction.
Building a model
All chromatography models comprise different parameters to determine the quantitative influence of the effects the model considers. Suppliers provide some model parameters, such as column dimensions and average adsorber bead sizes. Many suppliers have also recognized the influence of the material properties. For instance, Cytiva offers pre-characterized f(x) columns, which are delivered with detailed column-specific information (e.g., on porosities and lot-specific resin capacity).
The remaining protein-specific parameters need to be estimated from calibration runs. Today, the procedure is problem oriented and phase appropriate. For early process definition, when little sample material is available, three experiments can be sufficient to build a first model. Often, DoE experiments can be reused if at least one gradient elution is included. Commonly, the calibration is done using normal impure feedstocks and is based on chromatogram fitting using numerical optimization algorithms, as shown in Figure 2.
The goal of the calibration experiments is not to solve the separation problem but to understand the effects contributing to chromatogram shape, such as mass transfer limitations and the reaction to sudden changes in buffer composition. That is why, even for extensive process characterization studies, the number of calibration experiments rarely exceeds 10. Put simply, the number of relevant physico-chemical effects is limited.
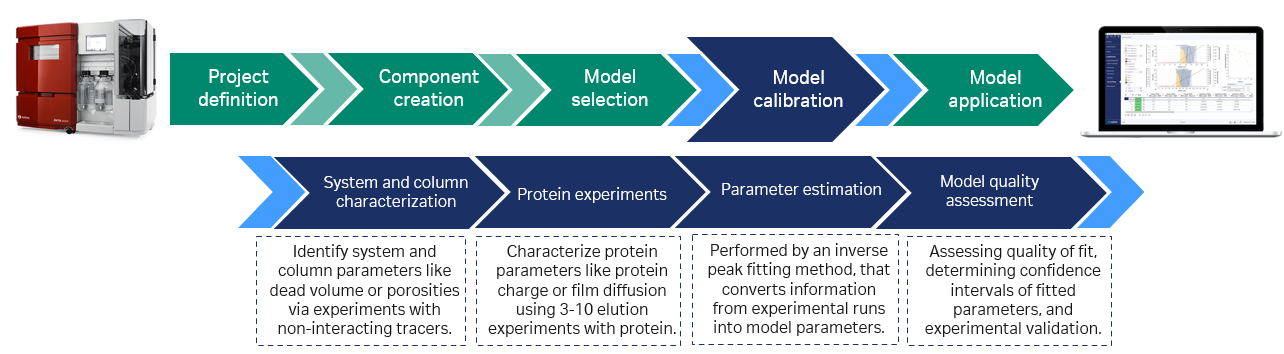
Fig 2. Model building is typically done using tracer runs with and without the column connected and bind–elute runs at conditions close to the intended set point. Based on these experiments an initial model is created. Additional information from offline analyses can be included. GoSilico™ Chromatography Modeling Software estimates the unknown protein-specific model parameters by curve fitting. After the in silico optimization, the process optimum is typically validated by one more experiment in the lab.
Model-based process development and optimization
The most obvious application of simulations is the prediction and optimization of existing processes. Figure 3 shows the development of a purification step for a virus-like particle using an anion-exchange membrane capsule. In contrast to column chromatography, the mobile phase is pumped through a cylinder formed by a spirally wound membrane. Three gradient elution runs with varying gradient slopes were sufficient for model building. Solely by computer optimization, a two-step elution was proposed and later validated by lab experiments. Here, process modeling clearly enabled the design of a selective, robust, and scalable process with minimal experimental effort for a complex feedstock (3).
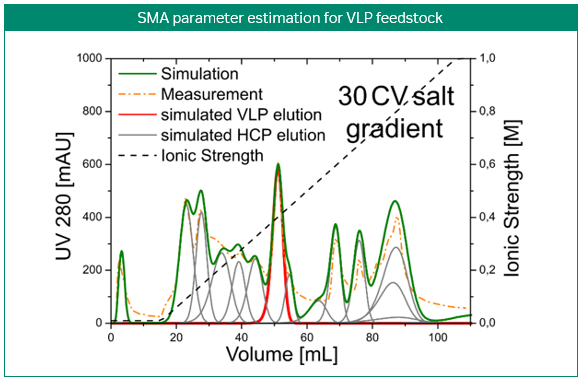
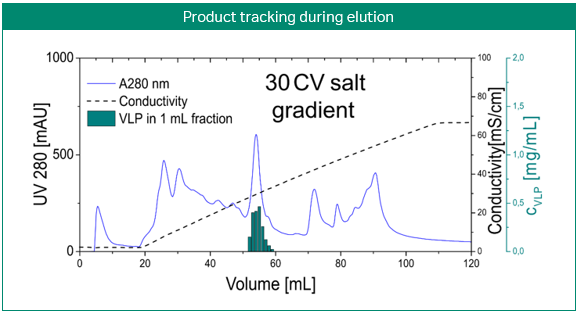
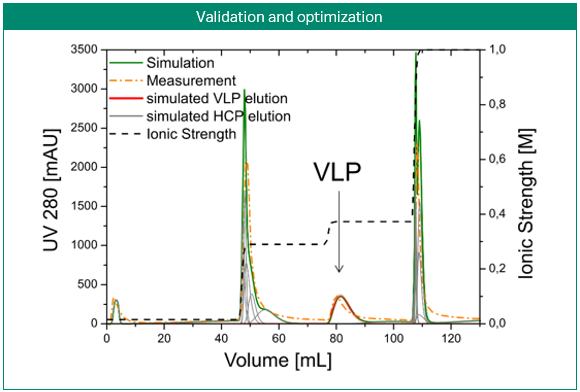
Fig 3. Development of a purification step for a virus-like particle using an anion-exchange membrane capsule. Model-based development of a capture step for an intermediate eluting virus-like particle (VLP; top). Calibration of the steric mass action (SMA) model, performed with three gradient elutions in GoSilico™ Chromatography Modeling Software (center). Using the model, a two-step elution was designed and successfully validated (bottom).
Linkage of steps and continuous chromatography
Bioprocess development typically involves independent optimization of each unit operation. For fully connected and continuous processes, a holistic development strategy is required. In connected downstream processing, each unit operation must tolerate process variations and raw material variability in all preceding operations. Traditional DoE studies are impractical, as the many critical parameters increase the experimental work exponentially while making it more difficult to gain process understanding.
Simulations are fast and cheap, enabling exploration of a high-dimensional design space in a reasonable amount of time. If models of two or more-unit operations are available, the operations are simply connected in silico and then analyzed or optimized as a single unit operation. This holistic optimization approach provides a global optimum for the connected process in terms of performance and robustness. A case study demonstrated the superiority of this approach for two consecutive ion-exchange chromatography steps (4). The authors showed that individually optimizing each unit operation can lead to a suboptimal overall process.
Mechanistic models can also provide a strategy to convert from batch to continuous operation modeling, because the physical principles are the same for single-column and multi-column setups. The continuous multi-column setup can be evaluated in silico to find optimal process conditions and to assess and optimize the time the system needs to reach steady state.
Scale up, scale down
Computer models can also be utilized for in silico scaling of a process from lab to pilot, or even production, scale. The fundamental assumption of this in silico scale up and scale down of chromatography is that only the fluid dynamics outside the pore system change; the effects inside the pore system are assumed to be scale independent. Once a sample component enters the pore system, diffusion, adsorption, and desorption follow the same mechanisms, whether in an adsorber bead packed in a filter plate or in a production column. Case studies have shown that the thermodynamics are scale-invariant (5). A prediction of the complete process on a new scale requires knowledge only of the basic fluid dynamic properties that can be derived from, for example, column qualification runs. This changes, to some extent, how to work with miniature columns as scale-down models. Properties of the chromatogram, such as peak broadening and even the resulting quality attributes, are understood to differ from the at-scale process. A model-based understanding of scale differences allows translation from one scale to another.
Simulation as a solution
Chromatography modeling tools have evolved to a state where they can replace laboratory experiments by inexpensive and fast computer simulations, reducing time and lowering costs. The low number of lab experiments needed to set up a model and the short simulation time enable development activities to proceed in parallel. Because first-principle models are employed, process understanding is captured within a model and establishes a link between the process design space and product quality. Problems with subsequent unit operations can be anticipated and corrected earlier. Accordingly, fully developed digital twins are likely to play an important role in handling raw material variability, batch control, and real-time release testing in the future.
Learn more on mechanistic modeling
References
- EMA. Questions and answers on design space verification. EMA/603905/2013 24 October 2013. https://www.ema.europa.eu/en/documents/other/questions-answers-design-space-verification_en.pdf.
- Kelly B. Quality by Design risk assessments supporting approved antibody products. mAbs 2016; 8(8): 1435-1436.
- Effio CL, Hahn T, Seiler J et al. Modeling and simulation of anion-exchange membrane chromatography for purification of Sf9 insect cell-derived virus-like particles. Chromatogr A. 2016;1(429): 142-154.
- Huuk TC, Hahn Y, Osberghaus A, Hubbuch J. Model-based integrated optimization and evaluation of a multi-step ion exchange chromatography. Sep. Purif. Technol. 2014; 136:207-222.
- Huuk, T, Hahn T, Griesbach J, Hepbildikler S, Hubbuch J. Scalability of mechanistic models for ion exchange chromatography under high load conditions in Extended reports: High-throughput Process Development.10–13. Cytiva. CY13184-11Dec20-BR. 2020.