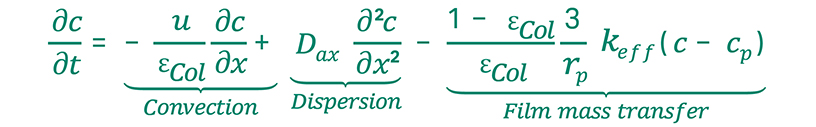Creating a predictive model of your downstream process using mechanistic chromatography models based on natural science
Each downstream purification step is comprised of different physical and biochemical effects. Chromatography for example is a complex superposition of general flow and transport patterns, mass transfer phenomena in microporous materials, and adsorption. Creating a predictive model of your downstream process therefore requires a profound consideration of all occurring effects.
How do mechanistic models work?
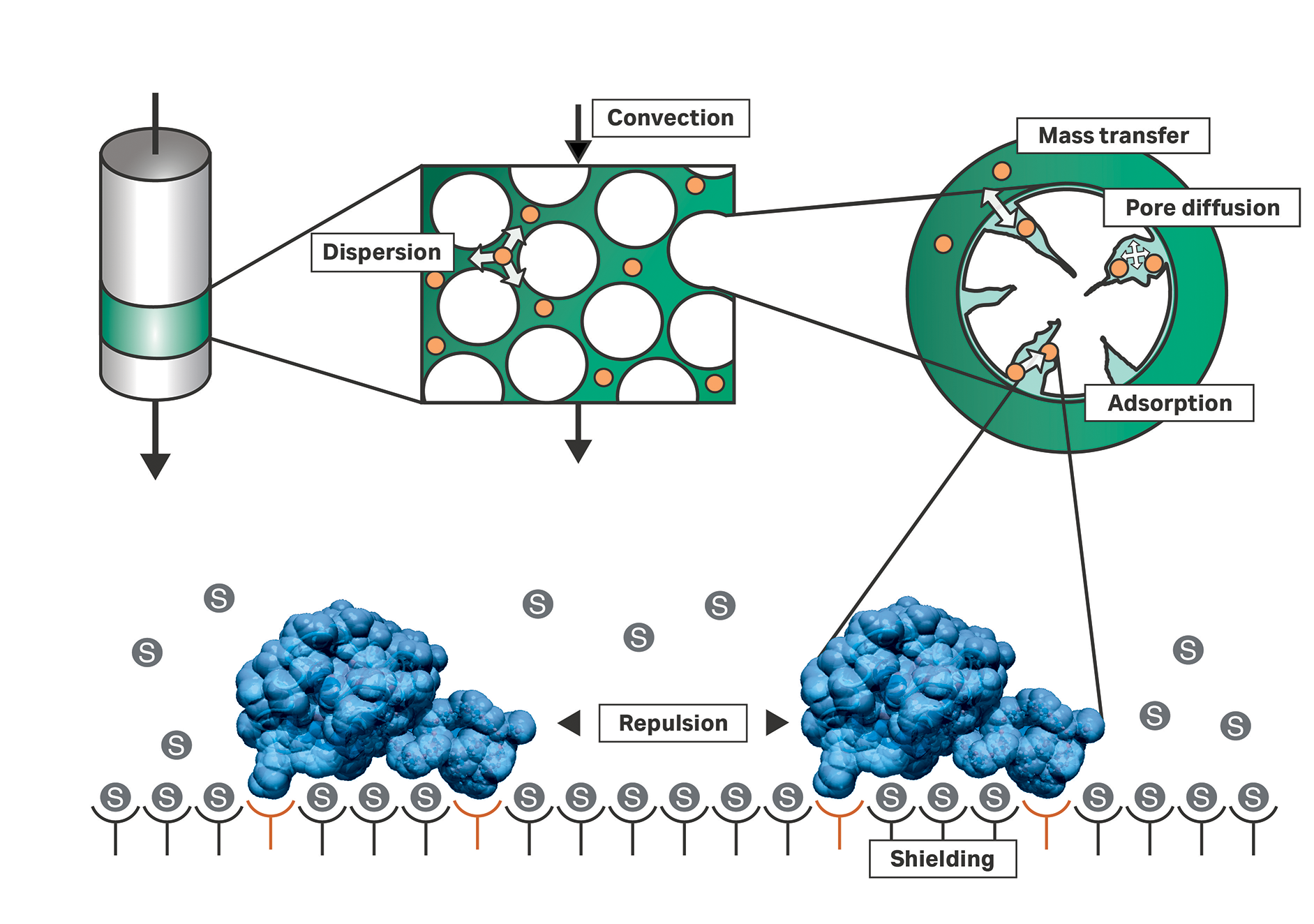
Mechanistic models consider physical and biochemical effects by means of natural laws. Outside the adsorber beads within a chromatography system for example, the injected components are transported by convection, which is induced by a connected pump. Dispersion comprises, among other effects, molecular diffusion and non-ideal flow. Inside the pores of the adsorbing particle, diffusion dominates their movement. Finally, the component is adsorbed onto the inner surface of the particle.
Fig 1. Depiction of the basic principles in the chromatography column
Building a predictive chromatography model
In order to predict any kind of downstream process, the governing natural principles must be described in mathematical model equations. In fact, column chromatography models comprise three individual but coupled models: a fluid dynamics model, describing general flow and transport patterns in the in the column, a model to describe the fluid phase within the beads’ pores, and an adsorption isotherm that models the adsorption process via thermodynamics. A large variety of such models are known in literature, describing different chromatography and interaction modes. Given the model and corresponding model parameters, the resulting chromatogram can be predicted by means of computer simulation.
Fig 2. Basic chromatography model equations
Few experiments are needed to calibrate your mechanistic model
Within mechanistic model equations a number of model parameters are inherent. Some of these are known, such as the column dimensions or flow rates for a chromatography model. Unknown model parameters such as protein charge must be derived from experimental data. Since each model parameter has a unique purpose and effect on the result, the required experimental data is small and usually ranges from three to ten. These experiments do not require purified components but can be performed using impure feedstock. The measured data are then processed in silico using numerical optimization to derive the unknown parameters by inverse curve fitting.
Once calibrated, any mechanistic downstream model is a fully equivalent digital twin of your real system. A simulated experiment can thereby replace a real experiment. The most obvious application of simulation is to optimize existing processes. In conjunction with Process Analytical Technologies (PAT) and real-time information on the composition of raw materials, downstream models can be expanded to become digital twins of running production processes.
Read more: