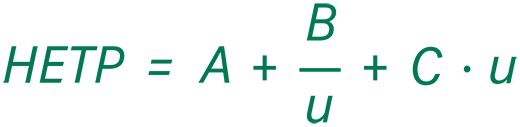Fluid flow induced by a connected pump plays an essential role in chromatographic separation. This flow naturally differs from column to column and resin to resin. However, this does not mean that an individual flow pattern must be calculated for the successful prediction of chromatography processes.
Flow patterns are three-dimensional in space. Chromatography fluid dynamics (CFD) models should be three-dimensional in space as well. However, 3D models are extremely complex to handle because:
- The experimental effort to analyze the exact geometry of the packed bed including cracks and void volumes is extremely high.
- The computational power needed to simulate a three-dimensional model grows with the cube of the mesh refinement and the demands quickly become enormous.
- The model complexity chosen to simulate a specific chromatography application may not even display three-dimensional effects.
Van Deemter: from 3D to 1D models
The good news is, 3D CFD simulations are not needed for the successful prediction of a chromatographic separation process. In fact, the performance of chromatography columns is sufficiently well described by a single parameter, the height equivalent to a theoretical plate (HETP). The van Deemter equation relates the HETP to the different contributions causing peak broadening within a chromatographic column:
- u – linear velocity
- A – eddy diffusion
- B – axial diffusion
- C – mass transfer between the interstitial, pore volume, and inside the stationary phase.
The physical principles in a chromatography column
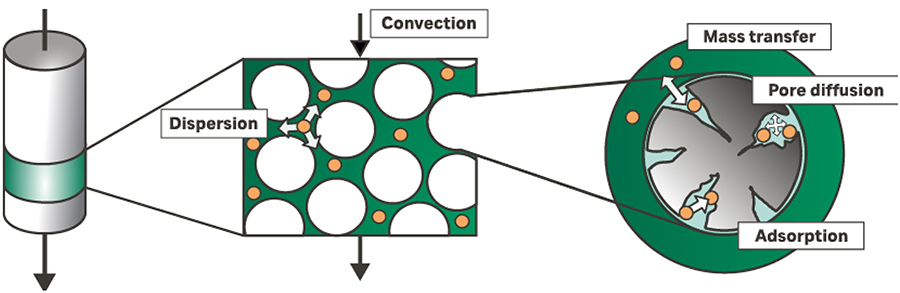
Mechanistic chromatography models are based on mathematical descriptions of the occurring physical and biochemical phenomena in a column. Figure 1 depicts these basic driving mechanisms within a chromatography column, with dispersion combining eddy diffusion and axial diffusion from the van Deemter equation.
Fig 1. The basic principles within a chromatography column.
Convection
Convection is induced by a connected pump. Pumping with a higher velocity leads directly to a larger convection inside the column. Taking a closer look, the linear velocity (distance per time) decreases with a bigger cross-sectional area. Therefore, the interstitial velocity is reversely proportional to the diameter of the tube.
Another factor influencing the linear velocity is the porosity of the particle bed or membrane. As the flow must move around the stationary particles or through the membrane, only a fraction of the column volume is available for flow. This flow is naturally greater than the induced velocity and has a reverse correlation to the porosity.
Axial dispersion
Dispersion combines the two terms in the van Deemter equation accounting for random molecular diffusion and non-ideal flow patterns causing turbulence. The result on the chromatogram is peak broadening which is modeled using Fick’s first law of diffusion along the column. In the case of strong flow rate changes during a run, the Fick diffusion coefficient can be divided into constant and velocity-dependent parts in line with van Deemter’s equation. Compared to the convectional effects, dispersion has a greater influence on the chromatogram shape.
Film mass transfer
While axial dispersion accounts for two effects in the van Deemter equation, the remaining term is modelled with film mass transfer and pore diffusion considered separately. A sufficiently small component can pass a particle’s stagnant fluid film and enter the mobile phase within the particle’s pore volume. The mass transfer towards the adsorbent surface through the film depends on particle and molecule properties and the concentration gradient. The film transfer also influences the peak broadening. A slow mass transfer leads to the effect that some molecules pass the particle without entering the pores. Other molecules stay in the pore longer as the transfer back to the interstitial volume is equally slow. This different behavior enhances peak tailing.
Pore diffusion
Once a component has entered a particle’s pore, its movement is dominated mainly by diffusion. The diffusion in the liquid is again described by Fickian diffusion. The pore diffusion coefficient depends on the characteristics of the stationary and mobile phase as well as the molecule. Another effect that enhances the observed diffusion is diffusion on the surface of the stationary phase. This can occur in parallel or separately. With surface diffusion, the molecule is adsorbed and moves flexibly over the surface. Because the thermodynamic interaction is often stronger than the diffusion effects, surface diffusion is often neglected or lumped into the pore diffusion coefficient.
Adsorption
Eventually, the component can be adsorbed onto the inner surface of the particle. For a more detailed description of protein adsorption, refer to the isotherm models section.
From physical principles to mechanistic models
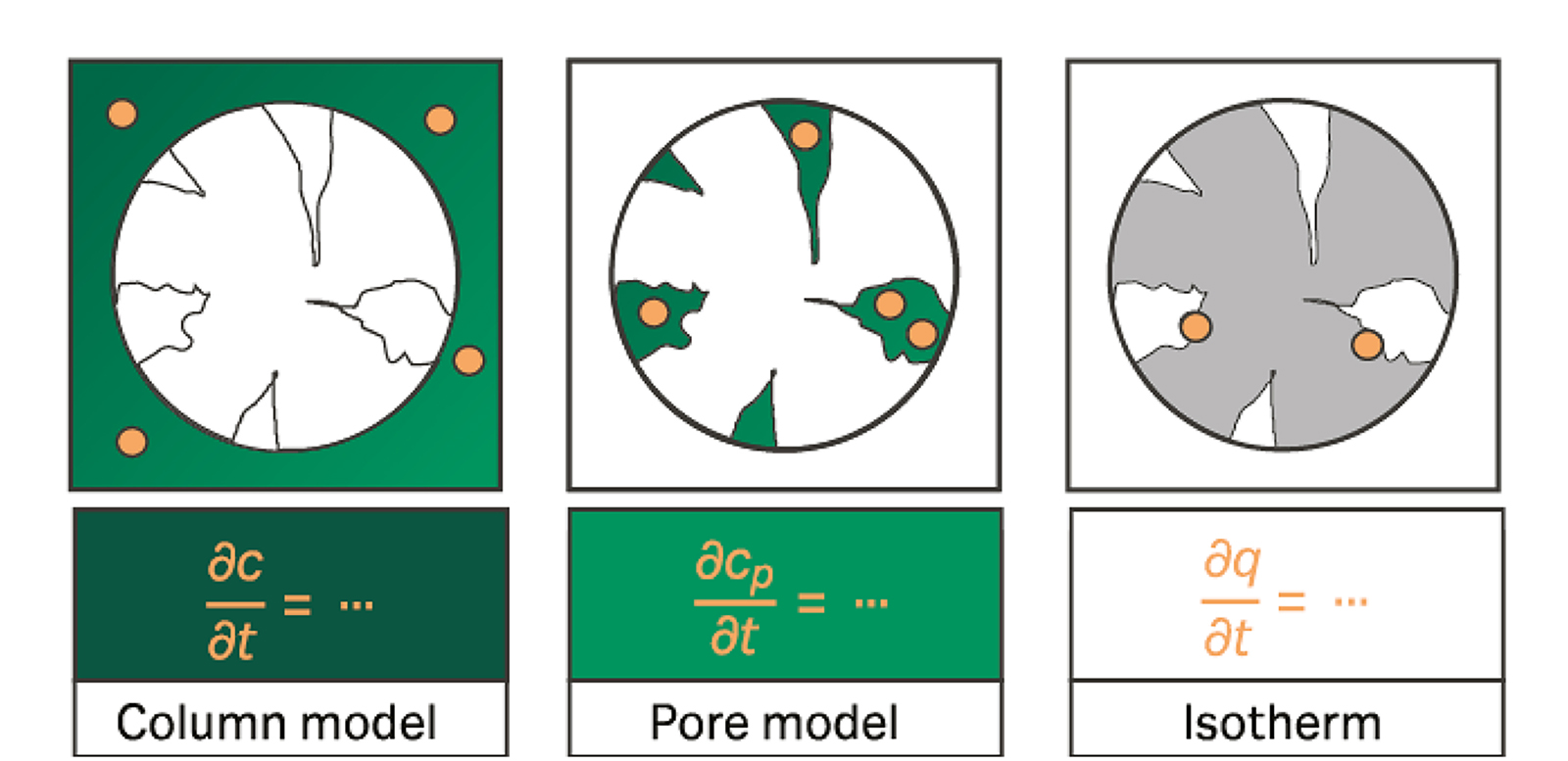
There are a variety of models for the mathematical description of liquid chromatography. Mechanistic models capture the change of molecule concentrations along their journey from interstitial volume of the mobile phase, to the pore volume of the mobile phase and finally to the volume of the stationary phase.
Mechanistic models of a chromatographic process are assembled with one model equation regarding column effects (column model), one considering the fluid phase within the beads’ pores (pore model), and one handling the adsorption process (isotherm model). A variety of models are described in literature, which are distinguished by the amount of separate physical effects they take into account.
Equilibrium dispersive model
The equilibrium dispersive model is a very basic column model that includes the effects of convection and dispersion to describe the concentration transport in the mobile phase. Additional fluid in a potential microporous volume is not considered explicitly. The whole fluid in a cross section of the column is said to be in equilibrium. Hence, this model is not suitable for materials with microporous volumes like membranes and monoliths or particles with fast mass transfer properties
Transport dispersive model and lumped rate model
Like in the Equilibrium Dispersive Model, convection and dispersion are used to describe the concentration transport in the interstitial volume. Additionally, the fluid volume inside the pores may have a different concentration than on the outside. Molecules are transported between the volumes at a finite rate. However, the effect of pore diffusion is not accounted for, so only an average concentration in the pores is calculated. A lumped mass transfer coefficient describes the combination of both effects
Note: Different textbooks use the above terms with different meanings.
General rate model
The general rate model is the most detailed model with the highest accuracy. It is suitable for adsorption of solutes with complex mass transfer and adsorption behavior. The general rate model considers mass transfer and pore diffusion separately. An additional diffusion sub-model describes the concentration transport in the liquid within the pores from the outside to the center. The model includes a film transfer coefficient and a pore diffusion coefficient. Due to the easily penetrable pores of modern chromatography resins, the film transfer coefficient is often less influential than the pore diffusion parameter. The diffusion model assumes spherical beads. Thus, the pores are approximately conical. The result is an asymmetric diffusion being fast near the center of the bead where less volume remains in comparison to the outside direction.